문제
- 밑면이 정사각형인 직육면체 벽돌들을 사용하여 탑을 쌓고자 한다. 탑은 벽돌을 한 개씩 아래에서 위로 쌓으면서 만들어 간다.
- 아래의 조건을 만족하면서 가장 높은 탑을 쌓을 수 있는 프로그램을 작성하시오.
- (조건1) 벽돌은 회전시킬 수 없다. 즉, 옆면을 밑면으로 사용할 수 없다.
- (조건2) 밑면의 넓이가 같은 벽돌은 없으며, 또한 무게가 같은 벽돌도 없다.
- (조건3) 벽돌들의 높이는 같을 수도 있다.
- (조건4) 탑을 쌓을 때 밑면이 좁은 벽돌 위에 밑면이 넓은 벽돌은 놓을 수 없다.
- (조건5) 무게가 무거운 벽돌을 무게가 가벼운 벽돌 위에 놓을 수 없다.
입력
- 입력 파일의 첫째 줄에는 입력될 벽돌의 수가 주어진다. 입력으로 주어지는 벽돌의 수는 최대 100개이다.
- 둘째 줄부터는 각 줄에 한 개의 벽돌에 관한 정보인 벽돌 밑면의 넓이, 벽돌의 높이 그리고 무게가 차례대로 양의 정수로 주어진다.
- 각 벽돌은 입력되는 순서대로 1부터 연속적인 번호를 가진다. 벽돌의 넓이, 높이 무게는 10,000보다 작거나 같은 자연수이다.
출력
- 첫 번째 줄에 가장 높이 쌓을 수 있는 탑의 높이를 출력한다.
입출력 예제

풀이방식
이번 문제는 동적 계획법(dynamic programming)에 대한 문제이다.
동적 계획법 이란 시간 복잡도가 큰 문제를 직관적으로 작게 나눈다. 이렇게 나누어진 작은 문제들을 메모이제이션을 사용해서 최종적으로 본래 문제의 해결방안을 찾는 것을 말한다.
설계과정
1. Brick 객체를 생성해서 arr[ ] 에 각 벽돌의 정보들을 넣는다.
2. arr[ ] 배열을 벽돌 밑면 넓이 기준으로 내림차순 정렬한다.
3. dy[ ] 배열의 0번째에는 밑면 넓이 순으로 정렬되었으므로 그보다 더 아래에 올 벽돌은 없기 떄문에 0번쨰 벽돌의 높이를 저장한다.
4. i-1 부터 0까지 감소하면서 j 번째 벽돌의 무게가 i 번째보다 무겁고 dy[ j ] 가 최대 높이보다 크다면 최대 높이를 dy[ j ] 로 변경한다.
5. 그 후 dy[ i ]에 최대높이와 현재 벽돌의 높이를 더해서 저장한다.
6. 마지막으로 result와 dy[i]중 큰 값을 찾아서 result에 넣고, result를 출력한다.
풀이과정
1. 각 변수들을 선언한다.
- arr[ ] : 벽돌의 정보들을 저장한다.
- dy[ i ] : i 번째 벽돌이 제일 위에 있을 때, 탑의 최대 높이를 저장한다.
- max_h : 최대 높이를 저장한다.
- s : 벽돌 밑면 넓이
- h : 벽돌 높이
- w : 벽돌 무게
2. arr[ ] 배열을 밑면 넓이를 기준으로 내림차순 정렬한다.
3. dy[ ] 배열 0번째에 arr.get(0).h 를 저장한다. 그리고 그 값을 result에 저장한다.
- s(밑면 넓이)를 기준으로 정렬되어있으므로, 0번째 넓이보다 큰 것은 없기에 해당 벽돌의 높이를 저장한다.
4. i - 1부터 0보다 크거나 같을때까지 감소하는 for문 안에 무게와 높이가 최대보다 크면 최대값을 바꿔주는 if문을 작성한다.
- arr.get(j).w > arr.get(i).w : j 번째 무게와 i 번째 무게를 비교해서 j 번째가 더 큰지 확인한다.
- dy[ j ] > max_h : 최대 높이인 max_h가 dy[ j ] 보다 작은지 확인한다.
- 위 조건이 전부 맞다면 max_h에 dy[ j ] 값을 넣는다.
5. 그 후 dy[i]에 max_h + arr.get(i).h을 넣어준다.
- 구한 높이를 현재 벽돌의 높이랑 더해서 현재 벽돌이 꼭대기일 때의 최대 높이를 구한다.
- 문제 예시를 통해 자세한 과정을 알아보자.
- 아래는 입력받은 arr 배열과 코드를 전부 수행한 후의 dy 배열이다.
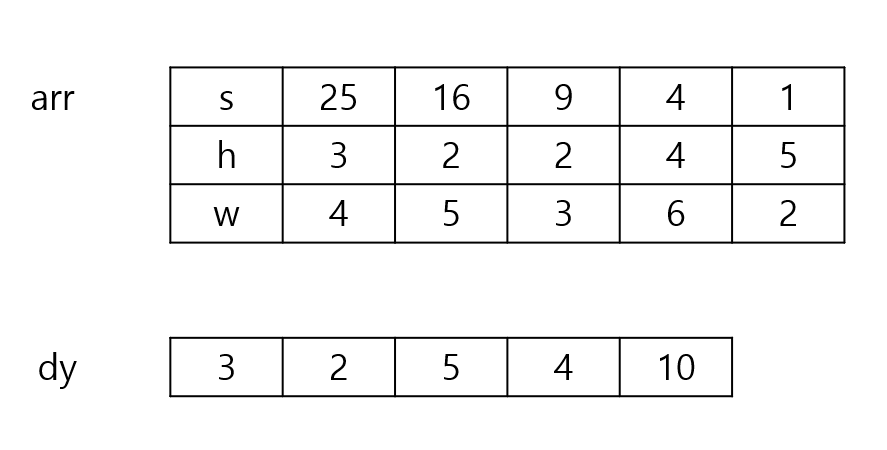
- 먼저 dy[0]은 3이다. 내림차순 정렬이기에 밑면 넓이가 25 보다 큰 것은 존재하기 않는다. 즉, 앞에는 다른 벽돌이 올 수 없다. 그러므로 해당 벽돌의 높이인 3을 넣는다.
- dy[1] 은 2이다. dy[1]의 무게는 dy[0]보다 커서 올라갈 수 없다. 그러므로 dy[1] 자체의 높이인 2가 최대 높이이다.
- dy[2] 은 5이다. dy[0]과 dy[1]에 다 올라갈 수 있다. dy[0]에 올라간다면 3 + 2로 총 5의 길이가 된다. 반면에 dy[1]에 올라간다면 2 + 2 로 총 길이 4가 된다. 결과적으로 둘 중에 더 큰 5를 넣는다.
- dy[3] 은 4이다. 더 큰 무게가 없어서 쌓을 수 없기에 스스로의 길이인 4로 넣는다.
- dy[4] 은 10이다. 모든 벽돌에 올라갈 수 있다. 모든 경우에 길이를 보면, 그 중 가장 큰 dy[2]에 5와 해당 벽돌의 높이인 5를 더해서 총 10을 넣는다.
6. Math.max() 를 사용해서 result와 dy[i] 중 더 큰 값을 result에 넣고, result를 출력한다.
해당 글은 인프런 > 자바(Java) 알고리즘 문제풀이 : 코딩테스트 대비(김태원)강의를 참고하여 작성하였습니다.
'알고리즘 > 인프런' 카테고리의 다른 글
| 섹션 10. dynamic programming(동적계획법) 6. 최대점수 구하기(냅색 알고리즘) (0) | 2023.01.26 |
|---|---|
| 섹션 10. dynamic programming(동적계획법) 5. 동전교환(냅색 알고리즘) (0) | 2023.01.24 |
| 섹션 10. dynamic programming(동적계획법) 3. 최대 부분 증가수열(LIS) (0) | 2023.01.20 |
| 섹션 10. dynamic programming(동적계획법) 2. 돌다리 건너기 (0) | 2023.01.19 |
| 섹션 10. dynamic programming(동적계획법) 1. 계단오르기 (2) | 2023.01.18 |



