https://www.acmicpc.net/problem/1644
1644번: 소수의 연속합
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
www.acmicpc.net
문제
- 하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다.
- 3 : 3 (한 가지)
- 41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지)
- 53 : 5+7+11+13+17 = 53 (두 가지)
- 하지만 연속된 소수의 합으로 나타낼 수 없는 자연수들도 있는데, 20이 그 예이다.
- 7+13을 계산하면 20이 되기는 하나 7과 13이 연속이 아니기에 적합한 표현이 아니다.
- 또한 한 소수는 반드시 한 번만 덧셈에 사용될 수 있기 때문에, 3+5+5+7과 같은 표현도 적합하지 않다.
- 자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하시오.
입력
- 첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
출력
- 첫째 줄에 자연수 N을 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 출력한다.
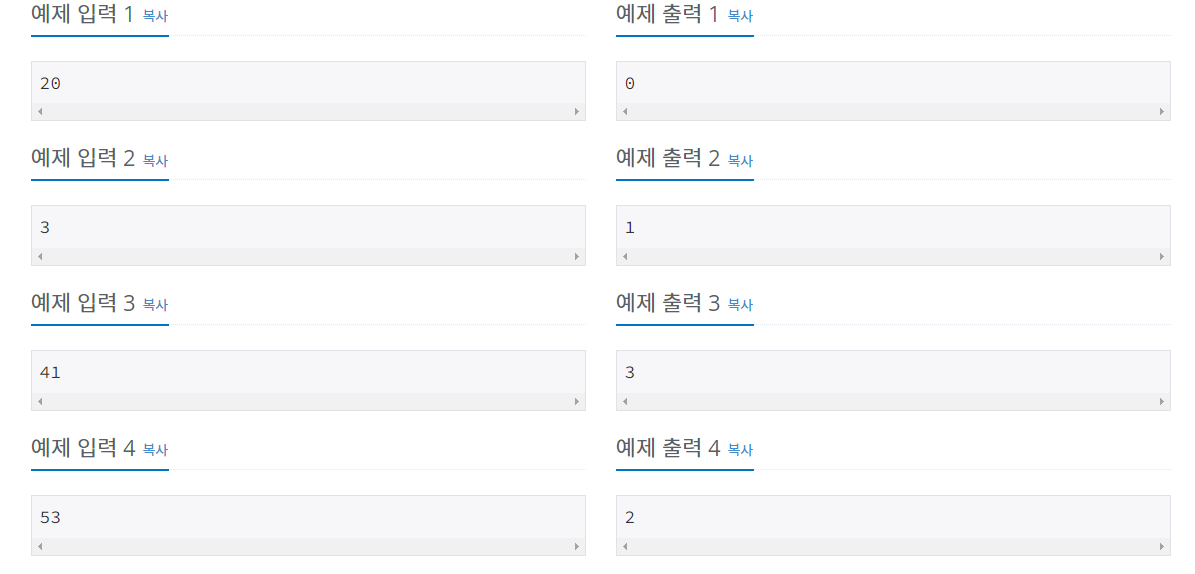
입출력 예제
풀이방식
답안소스를 보고도 이해가 안가서 한참 걸렸다
이번 문제는 소수와 투 포인터를 함께 사용하는 문제이다.
소수를 구하기 위해 에라토스테네스의 체를 사용하고, 해당 소수를 가지고 결과를 추출할 것이다.
에라토스테네스의 체
소수 관련 문제를 풀 때 가장 자주 사용되는 방법으로, 자세한 내용은 여기를 클릭한다.
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
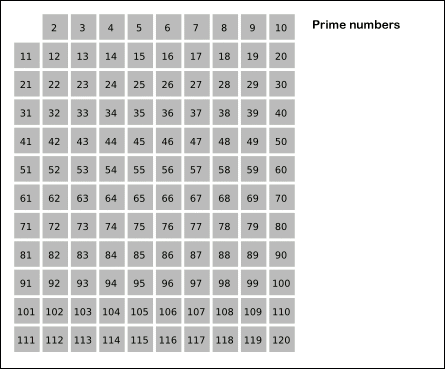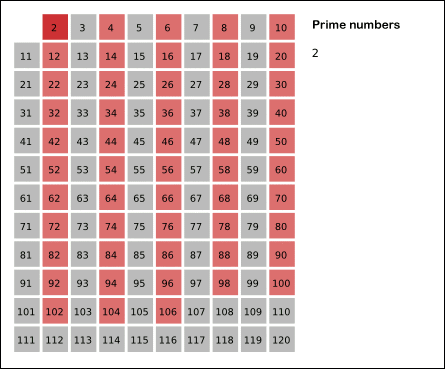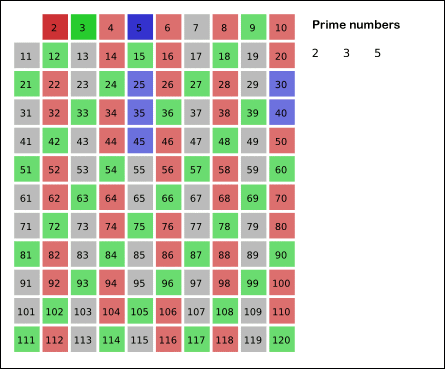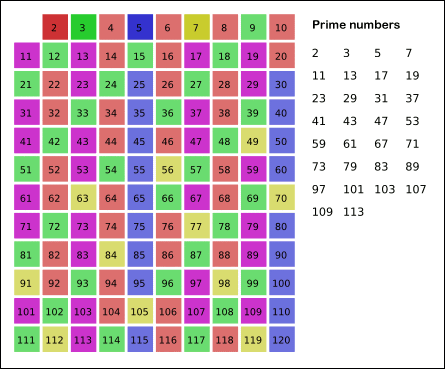
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
설계과정
1. 에라토스테네스의 체를 사용하여 자연수 N의 범위 안에서 소수를 찾아내고, 해당 소수들을 배열에 저장하는 메소드를 구현한다.
2. 메소드에서 구한 배열을 가지고 투포인터를 사용해서 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구한다.
풀이과정
1. 소수를 구하는 메소드를 구현하기 전에 전역으로 arr 배열을 선언한다.
- 메소드 뿐만 아니라 main에도 사용해야 하기 때문이다.
2. boolean 타입으로 isPrime[] 배열을 선언한다.
- isPrime[]에는 true는 소수가, false는 소수가 아닌 값이 들어간다.
- 이 때 배열의 크기를 N + 1 로 주어서 N까지 인덱스가 만들어질 수 있도록 한다.
3. Arrays.fill()을 통해서 isPrime에 true로 모든 값을 초기화한다.
- Arrays.fill() : 배열의 모든 값을 같은 값으로 초기화하는 메소드이다.
- Arrays.fill()을 사용하지 않으면 for문을 사용해서 배열의 값을 일정하게 초기화해야한다.
4. isPrime배열에 0번째와 1번째 인덱스 값에 false를 넣는다.
- 0번째와 1번째는 숫자 0과 1을 의미하고, 이는 소수가 아니므로 false를 넣는다.
5. 2부터 시작해서 자신의 배수가 되는 수들을 제외하는 for문을 작성한다.
- 2부터 시작해서 자신의 배수가 되는 수들을 false로 만든다.
- i * i 는 i의 배수인 값들을 소수에서 제외하기 위해서 작성한다.
- 예를 들어 i가 2이면, 2를 포함해서 2의 배수인 4, 6, 8 등의 수들을 전부 제외하기 위해서이다.
- 만약 53이라고 하면 8*8=64 이므로 2부터 8의 배수들만 지워도 된다.
6. isPrime이 true라면 즉, 소수이거나 i의 배수로 지워지지 않은 수라면 다음 작업을 추가로 진행한다.
- isPrime[i]가 true이면, i 이후의 i 배수는 약수로 i를 가지고 있는 것이므로 모두 true값을 준다.
- isPrime[i]가 false이면, i는 이미 소수가 아니므로 i의 배수 역시 소수가 아니게 된다. 그러므로 검사할 필요가 없다.
- j는 i의 배수가 되어야 하기 때문에 j += i 로 증가시킨다.
7. isPrime[i] 가 true 라면 소수이므로 arr에 추가한다.
- 배열명.add() : 배열에 새 요소를 추가한다.
8. arr 배열에 마지막으로 0을 추가한다.
- 투 포인터 탐색 시 끝까지 탐색할 수 있도록 하기 위해서이다.
9. 메인으로 넘어가서 메소드를 수행한다.
10. 연속된 소수의 합을 구하기 위해 필요한 변수들을 선언한다.
11. 각 포인터가 배열의 끝을 넘어가지 않도록 범위를 지정한 while 문을 작성한다.
12. sum이 N 보다 작으면 arr 배열에서 end 포인터 값을 가져와서 sum에 더하고, end 를 증가시킨다.

13. sum이 N과 동일하면 원하는 결과가 나온 것이므로 cnt를 증가시킨다.
14. 둘 다 아니라면 arr 배열에서 start 포인터 값을 가져와서 빼고, start 를 증가시킨다.
15. 마지막으로 cnt를 출력한다.
답안소스
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
public class Main {
static ArrayList<Integer> arr;
public static void prime(int N) {
boolean[] isPrime = new boolean[N+1];
Arrays.fill(isPrime , true);
isPrime[0] = false;
isPrime[1] = false;
for(int i=2; i*i<=N; i++) {
if(isPrime[i]) {
for(int j=i*i; j<=N; j+=i) {
isPrime[j] = false;
}
}
}
for(int i=1; i<=N; i++) {
if(isPrime[i]) {
arr.add(i);
}
}
arr.add(0);
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
arr = new ArrayList<>();
prime(N);
int start = 0;
int end = 0;
int sum = 0;
int cnt = 0;
while(start <= end && end < arr.size()) {
if(sum < N) {
sum += arr.get(end++);
} else {
if(sum == N) {
cnt++;
}
sum -= arr.get(start++);
}
}
System.out.println(cnt);
}
}'알고리즘 > 백준' 카테고리의 다른 글
| [백준 알고리즘 자바] 10773 : 제로 (0) | 2022.10.26 |
|---|---|
| [백준 알고리즘 자바] 10828 : 스택 (0) | 2022.10.25 |
| [백준 알고리즘 자바]1806 : 부분합 (0) | 2022.10.02 |
| [백준 알고리즘 자바]2470 : 두 용액 (2) | 2022.09.30 |
| [백준 알고리즘 자바]3273 : 두 수의 합 (2) | 2022.09.29 |



