반응형
▶ 기초통계량
1) 중심경향성 측면
- 산술평균 : 일반적인 평균 개념으로, 모든 값을 더한 후 데이터 개수로 나눈 값을 구하는 방식이다.
- 기하평균 : 모든 값을 곱하고, n 제곱근을 구하는 방식이다.
- 조화평균 : 액수의 산술평균을 구한 후, 다시 액수를 취하는 방식이다.
- 중앙값 : 데이터를 크기 순서대로 나열했을 때, 중간에 위치한 값을 말한다.
- 최빈값 : 데이터에서 가장 자주 나타나는 값을 말한다.
2) 분산 정도 측면
- 분산 : 각 데이터가 평균과 얼마나 떨어져 있는지를 나타내는 지표이다.
- 표준편차 : 분산에 제곱근을 취한 값을 말한다.
- 사분위수(IRQ) : 데이터의 상위 75%와 하위 25%의 중간 범위를 말한다.
3) 관계 측면
A. 공분산 : 두 확률변수의 상관정도를 말한다.
- 공분산 = 0
- 상관이 전혀 없는 상태
- 공분산 > 0
- 양의 상관관계
- 공분산 < 0
- 음의 상관관계
* 최소, 최대값이 없어 강약 판단이 불가능하다.
B. 상관계수 : 상관정도를 '-1 ~ 1' 값으로 표현한다.
- 상관계수 = 1
- 정비례 관계
- 상관계수 = 0
- 상관없음
- 상관계수 = -1
- 반비례 관계
C. 공분산과 독립성의 관계
- 두 변수가 독립이면 공분산은 0이지만, 공분산이 0이라고 두 변수가 독립이라고 할 수는 없다.
▶ 첨도와 왜도
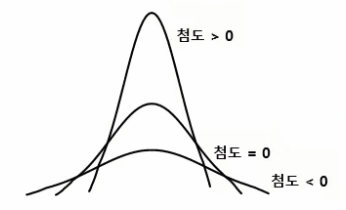
1) 첨도
- 자료의 분포가 얼마나 뾰족한 지를 나타내는 척도이다.
- [첨도 = 3] : 정규 분포 형태
→ 3을 빼서 0을 기준으로 정규분포 형태를 판단하기도 한다.
- 값이 클수록 뾰족한 모양을 한다.
1) 왜도
- 자료 분포의 비대칭 정도를 나타낸다.
- 왜도 = 0
- 대칭
- 왜도 < 0
- 최빈값 > 중앙값 > 평균값
- 평균값은 꼬리쪽을 따라서 간다. 다 더해서 데이터 개수로 나눈 것이 평균이기 때문이다.
- 왜도 > 0
- 최빈값 < 중앙값 < 평균값

→ 출처
반응형